Все приведенные выше числа, выражающие величину и массу Солнца, расстояния планет и размеры солнечной системы, основаны на точном знании расстояния, отделяющего Землю от Солнца.
Как вычислить это расстояние? Тот способ, который был применен для определения расстояния, на каком от нас отстоит Луна, неприменим в данном случае.
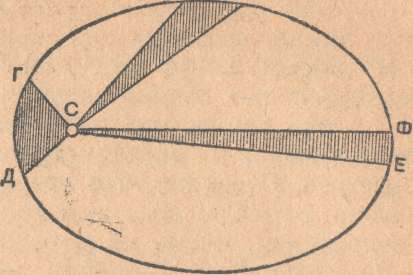
В самом деле, расстояние между нашей планетой и дневным светилом так велико, что прямые линии, проведенные от двух противоположных точек земного диаметра к центру Солнца, практически не составят треугольника,— эти линии сольются вместе, в одну, ввиду крайне ничтожных размеров земного диаметра по сравнению с огромным расстоянием, которое лежит между земным шаром и гигантом, управляющим движением планетной системы. Как составить треугольник ив земного диаметра и двух линий, соединяющих конечные пункты его с центром Солнца, когда этот диаметр по сравнению с длиной соединительных линий кажется не больше точки?
Это все равно, что пытаться начертить треугольник с основанием в 1 миллиметр, а боковыми сторонами — в 12 метров. Очевидно, что эти стороны должны быть практически параллельны, потому что углы, образуемые ими с основанием, очень мало отличались бы от прямого.
Знаменитый английский астроном Галлей, живший в XVII столетии, предложил для определения расстояния, отделяющего нас от Солнца, воспользоваться прохождениями Венеры мимо солнечного диска.
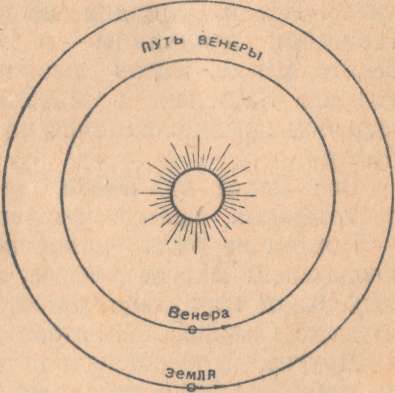
Мы видели уже, что Венера ближе к Солнцу, чем Земля, что она кружится по орбите, которая значительно меньше, чем орбита Земли. На прилагаемом рис. 41 обе орбиты начерчены в правильном масштабе.
В тот момент когда Венера проходит перед Солнцем, два наблюдателя, находящиеся па противоположных концах Земли, увидят ее в различных точках солнечного диска; разница в положении Венеры составит известный угол, а зная этот угол, можно вычислить расстояние до Солнца.
Рассмотрим внимательнее этот способ.
Два наблюдателя, А и Б (рис. 42), разместившиеся на противоположных концах Земли, смотрят на прохождение Венеры В перед Солнцем. Один из них увидит ее в точке B1, другой — в точке В2 на диске Солнца.
Проводя две прямые линии из этих точек к местам, где находятся наблюдатели, так, чтобы эти линии пересекались в той точке, где находится Венера, мы получим два треугольника. Основанием одного треугольника служит линия В1В2, а основанием другого — земной диаметр АБ. Оба треугольника имеют одну общую вершину в точке, где находится Венера.
Между сторонами этих треугольников существует известное соотношение на основании закона Кеплера; таким образом, вычислено, что сторона В1В2 относится к стороне АБ, как 1 :0,37; другими словами, земной диаметр составляет 0,37 линии, соединяющей обе точки прохождения Венеры.
Теперь вся суть в том, чтобы точно измерить угол, под которым видна эта линия. Если, например, найдено, что он равняется 48 секундам, то земной диаметр, рассматриваемый с Солнца, составил бы только 0,37 этого числа, то есть 48X^=17,76 секунды (17",76). Это и есть параллакс Солнца, или угол, под которым наша планета видна с Солнца.
А что такое секунда дуги?
Это есть видимая угловая величина метра или всякого другого предмета, удаленного от нас на расстояние, превышающее в 206 265 раз его длину.
Диаметр Земли виден с Солнца под углом не в одну секунду, а в 17,76 секунды, следовательно, расстояние Солнца от нас равняется не 206 265 земным диаметрам, а числу, меньшему в 17,76 раза, то есть 206265/17,76=11 614. Таким образом, расстояние Солнца от нашей планеты определяется длиной 11 614 земных диаметров.
Обыкновенно счет ведется не по диаметрам, а по полудиаметрам, то есть по земным радиусам, что нисколько не изменяет дела. Таким образом, параллаксом Земли будет считаться угол, под которым с Солнца виден радиус ее — 8",88, то есть 17",76, разделенное на 2. Числа 17,76, а следовательно, 8",88 взяты мною произвольно, ниже мы приводим истинные числа, выведенные на основании непосредственных наблюдений, которые производились различными астрономами.
Галлей, впервые предложивший воспользоваться прохождением Венеры мимо солнечного диска для определения расстояния, отделяющего нас от Солнца, сам лично не мог применить к делу свое предложение, потому что не мог видеть прохождения Венеры, явления, весьма редкого для нас.
Венера проходит перед Солнцем через каждые 113% лет, увеличенные или уменьшенные на 8 лет. Одно из прохождений Венеры наблюдалось, например, в декабре 1639 года. Следующее случилось в июне 1761 года, то есть ровно через 113%+8 риСт и. лет, или через 121% год после первого прохождения. Новое прохождение произошло через ПЗ1/^— 8 лет, то есть через 105% лет, именно в декабре 1874 года. Через 8 лет — в декабре 1882 года — снова наблюдалось новое прохождение Венеры перед солнечным диском. Следующее прохождение ее произойдет опять через 113У2 +8 лет, то есть через 121% год, значит, в июне 2004 года, затем снова через 8 лет и т. д.
Два последних прохождения Венеры — 8 декабря 1874 года и б декабря 1882 года — наблюдались научными экспедициями всех культурных народов; эти экспедиции были разосланы во все концы земного шара, где явление могло быть видимо.
Франция отправила свои экспедиции в Японию, Китай и Индо-Китай, в Новую Каледонию, на остров Святого Павла, на остров Кампбель (Тихий океан). Англия послала своих ученых в Индию, Египет, Сирию, Китай, Японию, на мыс Доброй Надежды и в Австралию.
Американцы заняли наблюдательные пункты в Сибири, Китае, Новой Зеландии, на островах Чатоме, Каргелене и Тасмании; итальянцы — в Бенгалии; немцы — в Персии, Египте, Китае, Новой Зеландии, на океанских островах, и островах Каргелене и Святого Маврикия; наконец, русские астрономы расположились по всей России вплоть до самой Сибири.
Все места на Земле, где могло наблюдаться явление прохождения, были вычислены заранее.
Погода не была одинаково благоприятна для всех наблюдателей: многие ученые, к своему огорчению, принуждены были вернуться домой, не только не увидев Венеры, но даже Солнца, вследствие дождя, лившего весь день.
Другие, наоборот, имели возможность благодаря чистому небу отлично наблюдать редкое явление и вернулись на родину, успев сделать массу измерений и фотографических снимков.
На память об этом событии и произведенных измерениях по постановлению французского национального института была выбита медаль.
На основании всех наблюдений, произведенных во время обоих прохождений в 1874 и 1882 годах, установлено, что величина измеренного параллакса Солнца колеблется в пределах 8",00—8",86. Под таким углом с Солнца виден полудиаметр Земли.
Кроме этого способа, существуют еще другие методы определения расстояния, отделяющего нас от блистательного светила. Все эти методы служат превосходным подтверждением вычислений, сделанных по способу, предложенному Галлеем.
Так, например, найдено, что свет, испускаемый Юпитером, достигает Земли в 30—40 минут, смотря по тому, на каком расстоянии эта планета находится от нас.
Далее обнаружено, что момент наступления затмения спутников Юпитера (когда они погружаются в отбрасываемую им тень или прячутся за его огромным телом) изменяется на 16 мин. 26 сек., смотря по тому, находится ли Юпитер по ту же сторону от Солнца, как и Земля, или же на противоположной.
Запаздывание на 16 мин. 26 сек. в одном случае по сравнению с другим вызвано тем обстоятельством, что свет должен пробежать еще расстояние, равняющееся диаметру земной орбиты; на прохождение же полудиаметра, или радиуса, то есть расстояния Земли от Солнца, свет должен употребить половину этого времени — именно 8 мин. 13 сек. Принимая во внимание, что скорость света, найденная из опытов различными физиками — Фуко, Физо, Корню, Ньюкомбом, — определяется в 300 тысяч километров в секунду, мы приходим к заключению, что расстояние Земли от Солнца равняется 149У2 миллионам километров.
Третий способ нахождения этого расстояния также основан на знании скорости распространения света в пространстве.
Мы упоминали уже о явлении, известном под именем аберрации, или отклонения света. Свет, идущий от светил, распространяется в пространстве, как мы знаем, с удивительной скоростью. Земля, в свою очередь, мчится по своей орбите, и сложение этих двух движений имеет своим результатом то обстоятельство, что мы видим светила не в том месте, где они действительно находятся, а несколько в стороне от действительно занимаемого ими положения.
Вычисления показывают, что наблюдаемая величина этого кажущегося смещения светил требует признать скорость света в 10 тысяч раз превышающей скорость Земли. Скорость движения Земли, таким образом, определяется в 30 километров в секунду; зная эту скорость, легко вычислить длину всего пути, пробегаемого Землей в течение года, а отсюда можно узнать, чему равняется диаметр этого пути, или орбиты; половина этого диаметра, или радиус, и составляет расстояние нашей планеты от Солнца.
Существует еще несколько способов определения расстояния Земли от Солнца, но мы на них останавливаться не будем. Скажем только, что из всех этих способов явствует, что параллакс Земли, или угол, под которым виден с Солнца экваториальный полудиаметр Земли, равняется 8*,80, что соответствует расстоянию в 149% миллионов километров.
Таковы результаты измерения расстояния Земли от Солнца. Это не плод пылкого воображения, не роман — это неоспоримая математическая истина, которую может проверить всякий.
Такие колоссальные расстояния трудно представить себе отчетливо. Чтобы помочь в этом отношении воображению, выразим пространство во времени.
Из пушки ядро вылетает со скоростью 500 метров в секунду; если ядро, неизменно сохраняя эту скорость, будет лететь по прямой линии, то оно прибудет на Солнце только через 9 лет 8 месяцев.
Далее, вообразим себе, что от Земли до Солнца проложен рельсовый путь. Курьерский поезд, мчащийся со скоростью 60 километров в час и пе останавливающийся нигде ни на секунду, достигнет Солнца через 140 миллионов минут, что составит 97 222 дня, или 266 лет. Если бы за проезд взималось по копейке с километра, то подобное путешествие, не считая продовольствия, стоило бы 1 миллион 400 тысяч рублей.
Известно, что всякое ощущение, прежде чем добраться до головного мозга, центра всякого восприятия, должно пробежать известное расстояние по нервам, а для этого требуется известное время, правда, очень небольшое. Обжегши или поранив палец, мы чувствуем боль не в то же мгновение, а на несколько долей секунды позже.
Опытным путем найдено, что скорость передачи раздражения по нерву составляет 28 метров в секунду. Теперь представим себе ребенка, имеющего такую необычайно длинную руку, что в вытянутом положении она касается
боль от ожога, прикоснувшись пальцами к раскаленному шару? Ровно через 167 лет. Он дожил бы до глубокой старости и успел бы давно умереть, прежде чем ощутил бы боль.
Зная расстояние, отделяющее нас от Солнца, мы можем теперь вычислить его истинные размеры.
Мы видели, что экваториальный диаметр Земли, рассматриваемый с Солнца» равняется 17",60. Диаметр Солнца, видимый с Земли, составляет 34",4; отсюда следует, что диаметр Солнца в 109 раз больше, чем диаметр Земли, то есть равняется 12 756 километрам X 109 =1 390 600 километрам.
Зная диаметр, легко определить поверхность и объем всякого шара. Поверхность Солнца определяется в 6 биллионов квадратных километров, а объем его — в 1 300 тысяч раз больше объема Земли, то есть около 1 390 000 биллионов кубических километров. Это число пишется так: 1 390 ООО ООО ООО ООО ООО.
Никакое самое пылкое воображение не может постигнуть значения этих колоссальных цифр.
Чтобы наглядно показать, какая громадная разница существует между объемами Солнца и Земли, делают следующее сравнение. В одной кружке ржи (литр) заключается около 10 тысяч зерен средней величины; в одном ведре (12,3 литра) их будет 123 тысячи, а в юу2! ведрах таких зерен будет 1 290 тысяч.
Итак, представьте себе, что перед вами лежит с одной стороны только одно зернышко ржи, а с другой — большая куча ржи из 10 1/2 ведер, и вы получите соответственные объемы Земли и Солнца.
Земля — ничтожная, жалкая песчинка по сравнению с таким гигантским шаром, как Солнце. Если прибавить к Солнцу или отнять от него величину нашей планеты, это все равно, как если бы стало одним зернышком больше или меньше в нашей куче ржи из 10% ведер; этого даже и заметить нельзя.
Нам остается еще коснуться веса Солнца. Мы упоминали уже, что Солнце тяжелее Земли в 331 950 раз.
Как это доказать?
Выше, когда речь была о Луне, мы видели, что тяжесть и всемирное притяжение — одна и та же сила. Ньютон открыл тождество между ними, определяя расстояние между концом прямой линии, которую пробежала бы Луна по истечении одной секунды, если бы она была свободна от притяжения Земли, и концом кривой, которую Луна действительно описывает под влиянием земного притяжения.
Расстояние это—1 1/3 миллиметра — составляет в точности то пространство, которое прошло бы каждое тело, если бы оно было поднято на такую высоту и затем предоставлено самому себе. Если бы, например, какой-нибудь аппарат поднял человека на высоту Луны (как Магомета, который утверждал, что будто бы ангел однажды схватил его спящего за волосы и перенес на Луну) и затем оставил бы его в пространстве, то человек под действием тяжести начал бы падать, но чрезвычайно медленно: в первую секунду он опустился бы всего на 1 1/3 миллиметра, но чем дальше, тем скорость его падения увеличивалась бы все больше и больше.
С какой первоначальной скоростью будет падать тело, если перевести его на ту высоту, где находится Солнце?
Мы знаем, что притяжение обратно пропорционально квадрату расстояния. На Земле каждое тело, предоставленное самому себе, падает вниз, повинуясь силе тяжести, с первоначальной скоростью в 4,9 метра. Расстояние Земли от Солнца составляет около 23 200 земных радиусов. Следовательно, на этом расстоянии первоначальная скорость падения составляет 49 метра/23 200 2=49 метра/538240000, это очень ничтожная величина, она равняется 9 миллионным долям 1 миллиметра. Это расстояние и прошел бы камень в первую секунду, если бы был поднят на высоту, где находится Солнце, и если бы подвергался силе притяжения одной только Земли.
Теперь посмотрим, чему равняется притяжение Солнца на том расстоянии, которое отделяет его от Земли.
Для этого употребим тот же способ, который Ньютон применил для определения силы протяжения Земли «на высоте» Луны. Если бы Земля была свободна от притяжения Солнца, она двигалась бы по прямой линии; на самом же деле она принуждена описывать кривую вокруг Солнца. Как велико расстояние между этой воображаемой прямой и кривой, описанной Землей в действительности, по истечении одной секунды?
Точными измерениями найдено, что эта величина составляет около 3 миллиметров.
Итак, сила притяжения Солнца относится к силе притяжения Земли, приблизительно как 3 миллиметра относятся к 9 миллионным долям 1 миллиметра, то есть как 30 : 0,00009.
Вычислив точно это отношение, находим, что сила притяжения Солнца больше силы притяжения Земли в 331 950 раз,—другими словами, Солнце притягивает тела во столько раз сильнее, чем Земля, и так как притяжение и тяжесть — одна и та же сила, значит, Солнце тяжелее Земли в 331 950 раз.
Есть еще другой вполне точный способ вычисления веса Солнца, основанный на том же принципе притяжения и законах Кеплера.
Мы знаем уже, что чем дальше планета отстоит от Солнца, тем медленнее вращается она по своей орбите. Закон Кеплера гласит, что квадраты времени обращения планет относятся, как кубы расстояний.
Предположим теперь, что Луна находится на том месте, где теперь находится Солнце. В какое время совершала бы она полный оборот вокруг Земли? 149% миллионов километров, отделяющих Землю от Солнца, составляют 385 расстояний Луны от Земли. 385 в кубе (3853) составляет 57 066 625; квадратный корень из этого числа (\/57 0 66 625 равняется 7 553. Значит, Луна на таком громадном расстоянии от нас двигалась бы по своей орбите в 7 553 раза медленнее, чем теперь, и для полного оборота вокруг Земли ей потребовалось бы 206 330 дней, то есть 566 лет. Итак, Земля имела бы силу заставить своего спутника совершить полный оборот вокруг нее в 566 лет, тогда как Солнце вращает Землю и Луну в 1 год; отсюда можно было бы сделать заключение, что Солнце в 566 раз «сильнее», то есть тяжелее Земли.
Но мы должны считаться в этом случае с квадратами расстояний, а квадрат 566 составляет круглым числом 320 тысяч.
Приняв во внимание и дроби расстояний, мы получили бы, как и в первом случае, число 331 950, показывающее, во сколько раз Солнце тяжелее Земли.
Разбирая вопрос математически, мы должны были бы указать на разницу, существующую между понятиями "вес" и "масса"; но мы думаем, что в популярном сочинении усложнять дело тонкостями бесполезно.
Зная объем и массу Солнца, мы легко можем определить плотность его. Плотность тела есть масса, разделенная на объем. Так как Солнце в 1 300 тысяч раз больше Земли, а тяжелее ее только в 331 950 раз, то из этого следует, что оно гораздо менее плотно, чем наша планета. Если плотность Земли принять за единицу, то плотность Солнца выразится числом 0 256; это значит, что вещества, входящие в состав Солнца, весят только 34 того, что весят вещества, образующие Землю.
