Движение Луны около Земли

Вследствие этого расстояние Земли от ее спутника ме­няется беспрестанно: наибольшее расстояние (в апогее) составляет 406 670 километров, наименьшее (в перигее) — 356 тысяч километров; среднее расстояние — 384 тысячи километров.

Это колебание в расстояниях имеет большое значение для солнечных затмений, которые вследствие этого бывают то полные, то кольцеобразные, а также отражается на си­ле морских приливов и отливов.

Движение Луны в пространстве еще более сложно, чем движение Земли. Орбита Луны не остается неподвижной в своей плоскости, — большая ось эллипса передвигается, описывая круг в 3 232 дня, то есть почти в 9 лет. Это пе­ремещение оси, как можно видеть, аналогично движению большой оси земной орбиты, которое совершается в 21 ты­сячу лет.

Далее, орбита Луны не находится в той плоскости, в которой Земля вращается вокруг Солнца, то есть не нахо­дится в эклиптике; в противном случае, если бы спутник Земли вращался вокруг нее в той же плоскости, в которой Земля кружится вокруг Солнца, то затмение Солнца про­исходило бы при каждом новолунии, а затмение Луны — при каждом полнолунии. Плоскость вращения Луны на­клонена к плоскости земной орбиты под углом в 5°. Ли­ния пересечения обеих плоскостей называется «линией узлов», и она не остается неподвижной, так как описывает круг в плоскости эклиптики в 6 793 дня, то есть в 18,5 года.

Угол, под которым плоскость лунной орбиты наклонна к эклиптике, также изменяет свою величину от 5°0'1" до 5°17'35" в течение каждых 173 дней.

Перечисление всех тех видоизменений, которыми харак­теризуется движение Луны в пространстве, завело бы нас слишком далеко. Достаточно заметить, что всех различных видоизменений, колебаний и уклонений, встречающихся на пути нашего спутника, насчитывается не меньше 66!

Вращаясь вокруг Земли, Луна в то же самое время следует за ней в ее движении вокруг Солнца. Какой же путь описывает Луна в пространстве? Если бы Земля бы­ла неподвижна, то Луна описывала бы вокруг нее простой эллипс, но Земля движется по своей орбите, а вместе с ней движется также и ее спутник.

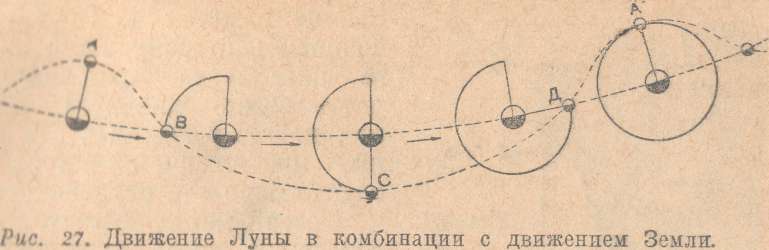
Из комбинации движения Луны вокруг Земли и дви­жения Земли вокруг Солнца слагается путь, пробегаемый Луной в пространстве. Этот путь имеет форму кривой, которую мы и приводим на рис. 27.

В то время как Луна из точки А перешла в точку В_, Земля успела уже передвинуться по орбите на расстояние и несколько миллионов километров. В точке В Луна на­ходится в первой четверти. Семь дней спустя Луна перехо­дит в новую фазу, — именно наступает полнолуние С; за это время Земля опять успела значительно передвинуться вправо. Еще через неделю Луна будет в третьей четверти, п точке Д; и, наконец, добравшись до точки А, Луна при- ходит и свое первоначальное положение, совершив полный оборот вокруг Земли. Соединив плавной линией точки А, В, С, Д, А мы получим кривую, изображающую путь, пробегаемый Луной в пространстве.

Мы зноем, каким образом Луна передвигается, знаем, на каком расстоянии она находится от Земли. Но теперь остается узнать, сколько весит Луна.

Вес Лупы можно найти, определив точно силу .притя­гательных воздействий ее на Землю. Главнейшими из этих притягательных воздействий являются приливы и отливы. Вода морей и океанов два раза в день подымается вверх, подчиняясь как бы молчаливому приказанию Луны. Зная высоту поднятия воды* можно определить, какая сила нуж­на была, чтобы совершить это поднятие, другими словами, можно вычислить силу притяжения, или вес тела, обу­словившего это воздействие на воду. Это один метод.

Второй метод основывается на влиянии, которое Луна оказывает на движение земного шара: когда Луна нахо­ди геи впереди Земли, она притягивает нашу планету и за­ставляет се двигаться скорее; когда же Луна находится позади Земли, она по-прежнему притягивает ее, но в об­ратном направлении, и таким образом несколько задержи­вает поступательное движение земного шара. Благодаря этому обстоятельству в то время, когда Луна находится в первой и последней четверти, Солнце кажется нам перемещенным в сторону на 3/4 своего параллакса, или на 1/290 часть своего диаметра. Зная это, можно вычислить вес Лу­ны, притяжением которой и обусловлено это отклонение.

Если бы Луна при той массе, которой она обладает теперь, имела объем, занимаемый Землей, то, принимая во внимание, что сила притяжения обратно пропорциональна квадрату расстояния, а радиус Луны в четыре раза мень­ше, чем радиус Земли, сила тяжести уменьшилась бы в 1G раз; таким образом, вес тел на Луне был бы в 90 раз меньше, чем на Земле. Человек, который на Земле весит 10 килограммов, на Луне весил бы в этом случае меньше килограмма, и того усилия, которое он употребляет на Зем­ле, чтобы вскочить на стул, было бы на Луне достаточно, чтобы перенести его на вершину очень высокой горы.

Возможно существование таких миров, которые отли­чаются такой ничтожной плотностью и такой быстротой вращения, что сила тяжести почти совершенно отсутствует на их поверхности, — там предметы не имеют почти ника­кого веса. И обратно, могут быть такие миры, плотности которых необыкновенно велики, так что все тела там имеют чудовищно большой вес. Представим себе, что Земля, не изменив своего объема, сделалась бы так же тяжела, как Солнце, тогда каждый килограмм весил бы 324 тысячи килограммов; молодая грациозная девушка, имеющая те­перь 50 килограммов весу, весила бы тогда 16 200 тонн.

Вот таблица силы тяжести по сравнению с земной, существующей на различных планетах:

Сила тяжести

Солнце.................................... 27,47 Уран . ................................................. 0,92

Юпитер.................................... 2,64 Венера.............................................. 0,85

Сатурн...................................... 1,17 Меркурий............................................... 0,27

Нептун.................................... 1,12 Марс...................................................... 0,38

Земля...................................... 1,00 Луна....................................................... 0,16

Таким образом, наибольший вес имеют тела на Солнце, наименьший — на Луне. Чтобы ясно представить себе эту разницу в весе, проследим, с какой скоростью падает с данной высоты одно и то же тело на различных планетах.