Луна представляет собой светило, наиболее близкое к нам. Как мы уже заметили раньше, Луна есть детище Земли, от которой она была оторвана действием центробежной силы в то отдаленное время, когда земной шар представлял собой туманную газообразную массу; вот почему Луну и называют иногда колонией земного шара.
Расстояние Луны от Земли составляет 384 тысячи километров. Это, в сущности, очень немного. Многие путешественники и мореплаватели проехали по железной дороге и на пароходах значительно большее расстояние, чем то, которое отделяет Луну от Земли.
Но кто может доказать, скажут некоторые, что вышеприведенное число километров, представляющее расстояние между Луной и Землей, соответствует действительности? Кто нас уверит, что астрономы не ошибаются в своих вычислениях?
Сомнение — вообще вещь похвальная, в соединении с любознательностью оно дает толчок прогрессу. Но в данном случае сомнения совершенно неосновательны. Астрономические вычисления отличаются необыкновенной точностью, несмотря на то, что измерения производятся с помощью зрительной трубы, а не посредством метра.
Основой всех астрономических вычислений, которые относятся к расстояниям, служит измерение углов. Когда приходится измерить предмет, к которому в силу каких-нибудь внешних препятствий невозможно непосредственно подойти, единственным способом измерить отделяющее его расстояние является измерение угла, под каким этот предмет нам представляется.
Известно, что чем дальше отстоит предмет, тем угол, под каким его видят, кажется меньше. Между величиной видимого угла и расстоянием существует обратное соотношение: чем угол зрения меньше, тем расстояние от предмета больше.
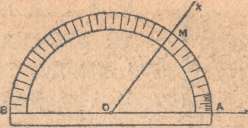
Каждый знает, что такое угол; каждый знает, что угол измеряется дугой, представляющей часть окружности. Полная окружность круга, как известно, делится на 360 частей, которые называются градусами.
Каждый угол делится на 60 частей, называемых секундами. Эти названия не имеют ничего общего с теми минутами и секундами, которыми мы привыкли измерять время. Градус изображается кружком (°), минута — одним значком ('), секунда — двумя (").
Если полная окружность круга равняется 360 сантиметрам, то на ней каждый градус равняется 1 сантиметру, каждая минута — 7°° сантиметра, а каждая секунда— V3600 сантиметра.
Известно, что чем дальше отстоит предмет, тем он кажется меньше. Доказано непосредственным опытом (который легко можно проверить), что если предмет, каких бы размеров он ни был, удален на расстояние, в 57 раз превышающее его диаметр, то угол зрения, под каким мы его видим, равняется 1°. Например, круг, имеющий в диаметре 1 метр, удаленный на расстояние 57 метров, виден под углом в 1°. Луну мы видим под углом в 31'8"; этот угол несколько больше У2°.
Если бы Луна была видима под углом, составляющим 1°, то это значило бы, что она удалена от нас на расстояние, превышающее ее диаметр ровно в 57 раз, но так как этот угол составляет всего 1/2 с излишком, то отсюда следует, что это расстояние почти вдвое больше, то есть превышает диаметр Луны примерно в 110 раз.
Угол, под которым виден с Луны радиус Земли, называется параллаксом Луны. Этот параллакс составляет 57' (почти 1°), поэтому расстояние Луны от Земли и составляет 601/4 полудиаметров, или радиусов, земного шара.
Радиус Земли равняется 6 371 километру; таким образом, расстояние Луны от нашей планеты определяется в 6 371 километр X 60*4 = 384 тысячам километров.
Высчитано, что пущенное с Земли пушечное ядро, которое летит со скоростью 500 метров в секунду, достигло бы Луны через 8 дн. 5 час. Если бы все пространство, отделяющее Землю от Луны, было залолнено воздухом, то взрыв вулканического извержения, происходящего на Луне, донесся бы до нас спустя 13 дн. 20 час. Поезд железной дороги, который мог бы пробежать вокруг Земли в 27 дней, добрался бы до Луны в 38 недель, если бы мчался с той же скоростью и не делал бы никаких остановок.
Радиусы Луны и Земли относятся друг к другу, как углы, под которыми они видимы, то есть как 15'34" : 57'. Отсюда легко можно вычислить диаметр Луны, — он равняется 3 476 километрам. Зная диаметр, можно определить окружность лунного шара и поверхность нашего спутника. Окружность его равна 11 070 километрам, а поверхность лунного шара равна 38 миллионам квадратных километров; это пространство в четыре раза больше, чем пространство, занимаемое Европой.
Луна делает полный оборот вокруг Земли в 27 дн. 7 час. 43 мин. 12 сек. со средней скоростью, равняющейся 1 017 мэтрам в секунду.
Наблюдения над движением Луны вокруг Земли привели Ньютона к открытию всемирного тяготения.
Рис. 24. От Луны до Земли - 30 земных диаметров
Между тем на небе показалась Луна. Молодой человек стал размышлять о том, какого рода должна быть сила, которая заставляет все тела стремиться к земле; он задал себе наивный, с первого взгляда, вопрос, почему Луна не падает на Землю, и, последовательно добираясь до причины, в силу которой Луна удерживается в небесном пространстве, он сделал одно из величайших открытий, которым справедливо может гордиться человеческий ум. Этот молодой человек был Ньютон. Закон всемирного тяготения, открытый им, дал ключ к разумению движений и равновесия, царящих во вселенной, и могучий толчок дальнейшему развитию астрономии как точной и обоснованной науки.
Как мы уже упоминали выше, тяжестью называется сила притяжения, влекущая каждый предмет вниз, к земле. Эта сила ослабевает по мере удаления от центра Земли. Поэтому если на поверхности Земли камень падает со скоростью 4,9 метра в первую секунду, то тот же камень, падая с высоты, на какой находится Луна, передвигался бы со скоростью 4,9 метра/602= 1,35 миллиметра, так как расстояние Луны от центра Земли равняется 60 земным радиусам.
Почему же все-таки Луна не падает? Да потому, что она, брошенная в пространство, как пушечное ядро, совершает в то же время круговое движение вокруг Земли. Это круговое движение развивает в ней центробежную силу, которая стремится оторвать Луну от Земли и умчать ее в пространство, но она этого не может сделать: отталкивание, вызываемое центробежной силой, и притяжение, оказываемое Землей, равны друг другу. Поэтому Луна не может ни улететь в пространство, ни упасть на Землю, а остается в равновесии. В этом положении ее удерживает та самая сила, которая заставляет все тела падать на землю. Отсюда до вывода, что равновесие всех небесных тел, рассеянных в пространстве, обусловлено взаимным тяготением, один только шаг. Это тяготение прямо пропорционально массе тел и обратно пропорционально квадрату расстояния их друг от друга.
То, что при этом происходит, можно было бы сравнить со следующим опытом. Вообразите себе, что вы вращаете рукой камень, привязанный на веревке. При его вращении также развивается центробежная сила, но камень удерживается натягивающейся веревкой.
Если веревку перерезать, то камень отлетит прочь по прямой линии, касательной к описываемому кругу и к той его точке, где камень был, когда веревку перерезали. В нашем примере натяжение веревки как бы заменяло притяжение Луны к Земле.
Например, два тела, из которых каждое имеет массу по 2 килограмма, притягиваются друг к другу вчетверо сильнее, чем два тела, каждое с массой в 1 килограмм, находящихся на таком же взаимном расстоянии. При сближении тел вдвое сила притяжения между ними возрастает в 4 раза, при сближении втрое она возрастает в 9 раз и т. д.
Английский физик Кавендиш, делая опыты со свинцовыми шарами, убедился в том, что тяготение действительно существует между всеми телами, где бы они ни были — в мировом пространстве или в лаборатории.
Если бы Луна перестала двигаться вокруг Земли, то, естественно, центробежная сила перестала бы развиваться; неминуемым последствием этого было бы то, что Луна немедленно упала бы на Землю. Я высчитал, что падение совершалось бы 4 дня 19 час. 54 мин. 57 сек. Мы предоставляем читателю судить о том, как отразилось бы на Земле и на ее обитателях падение такого громадного шара с такой ужасной высоты.
